囚徒的困境——惊天魔盗
你们到达之后会得到一张拍卖会邀请函,参加一场拍卖会,那是进入金库的必要条件,赢取更多的筹码吧,剩下的就看你的啦,千万不要让我失望,预祝咱们合作成功“。
精灵团建——惊天魔盗团
佘山庄园举行的精灵团建-惊天魔盗项目,学员们在这里学到了运用在工作和生活中非常关健要素的博弈,并且快乐地玩了一把密室挑脱和场景对抗。



经典桥段示例:
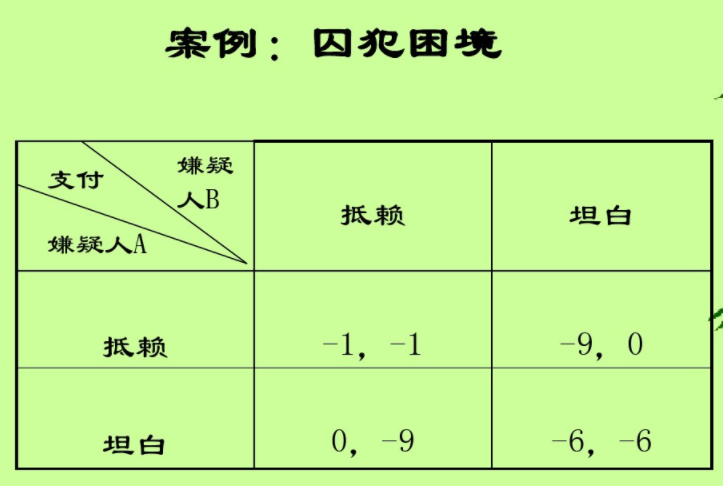
魔盗团队部份成员和安保部份成员因为斗殴被捕,安保开始分开审讯
双方都抵赖,都扣1币
双方都坦白,都扣6币
A抵赖,B坦白,A扣9币,B扣0币A坦白,B抵赖,A扣0币,B扣9币
如果两者都选择抵赖,双方就无罪释放。但因为彼此的相互怀疑,最终两个囚徒都会选择招供,这种情况就是博弈论中的“纳什均衡”,即选择对于自己最优的策略。但对两方最优的策略其实是都抵赖,

好,我们来看一下他们的选择思路。假设你是A,你现在不知道B会怎么选,所以你必须考虑B做出每一种选择可能给你带来的后果。
假如B选择了抵赖,那么你现在做哪个选择更划算呢?如果你抵赖,那你坐一年牢;如果你坦白,那么你可以不坐牢。所以如果B抵赖的话,你应该选坦白更划算。
假如B选择了坦白,那你的两种选择分别会带来什么样的后果呢? 如果你抵赖,那你要坐9年牢;如果你坦白,那你要被关6年。9年 v.s. 6年,那还是选坦白更划算。
于是,无论B做哪个选择,你都应该选择坦白更划算。于是,“坦白”便是A唯一合理的理性的,利益最大化,损失最小化的选择。
同样的道理,B也会选择坦白。这样一来,第二天早上我们这位聪明的检察官将会毫无悬念地得到两份认罪供述。
这个毫无悬念的结局就是经典囚徒困境的唯一答案(囚徒困境有其他条件变化而产生的变体,答案也随之会变化)。两个囚犯被这个游戏逼入了一个悲惨的困境,明明有一个“你好我也好”的可能,但是偏偏结果却必然是“你不怎样我也不怎么样”。而这个必然的结局就是著名的“纳什均衡点”。

刚看到这个问题,举一个最近比较火的游戏例子-绝地求生。
玩过的人都遇到过一个经典的场景: 你经过一路翻山越岭、杀人越货坚持到了最后的关键时刻,这个时候还剩一个敌人,但是新的安全区并不在你这里,你和敌人清楚的知道对方都在一棵树后面,然后去往安全区的路上空空如也。 这个时候,双方都不知道彼此的打算,但你们有个共同的目标,就是赢。 双方都有以下几种选择:
1、原地等待,让对方先冲出去然后打他
2、原地等待,让他先冲出去然后趁他疲于奔命的时候跑到安全区隐蔽
3、率先以风骚的走位,边走边跳,S形走位,走走停停,扔烟雾,或者直接狂奔到达安全区
4、伸出头瞄准对方可能的暴露点,吸引他出来,准备和对方火拼,或者直接扔炸弹
当然,你还有更多的选择,这个游戏很自由,不同的资源、不同的位置、不同的性格、不同的时机你都可能做出不同的选择,但是,这就面临一个问题,哪个才是你的最优解。 要解决这个问题,要提到一个概念:纳什均衡 就是说,此时此刻,双方僵持不下,谁不都愿意打破平衡率先行动,形成了一种静态平衡。但是,别忘了一件事情,毒圈还有5秒钟就开始缩小了,再不跑或者分出胜负,你的血量支撑不起毒圈造成的伤害,必定死亡。那么毒圈会打破这个平衡,强迫双方快速做出决定,这个时候你就必须综合各种条件,进行判断。 而平衡打破后,双方决策的组合就会产生相应的囚徒困境结果,以不同的收益结束,当然,无非就是你死我活的零和博弈。
